本文探讨了Python脚本与动态模态分解(DMD)的结合应用。我们将利用Python对从OpenFOAM模拟中提取的二维切片数据进行DMD计算。这种方法能够有效地提取隐藏的流动模式,深化对流体动力学现象的理解。
使用开源CFD软件OpenFOAM,有两种方法可以对CFD数据进行DMD计算。第一种方法是直接将OpenFOAM的场数据读入Python;第二种方法则是从OpenFOAM中提取二维切片,然后对这些数据进行DMD计算。
本文将重点介绍第二种方法,即利用Python的强大库直接分析从OpenFOAM提取的二维切片数据,执行DMD并可视化提取的模态。
OpenFOAM案例模态分解准备指南本研究的起点是雷诺数为100的方形圆柱周围完全发展的、统计稳定的流动。在此基础上,我们将模拟时间延长至100个涡脱落周期。在每个脱落周期内,我们从数据中提取16次二维切片。二维切片的提取是通过OpenFOAM中的surfaces函数对象实现的,具体配置如下:
surfaces { type surfaces; libs ("libsampling.so"); writeControl timeStep; writeInterval 142; surfaceFormat vtk; fields (p U); interpolationScheme cellPoint; surfaces { zNormal { type cuttingPlane; point (0 0 0.05); normal (0 0 1); interpolate true; } }; }; // ************************************************************************* //
模拟完成后,在案例的postProcessing目录中会生成一个名为surfaces的子目录,其中包含所有提取的表面数据。目录结构如下:
surfaces/ ├── 4771.2000000577236 │ └── zNormal.vtp ├── 4772.6200000577546 │ └── zNormal.vtp ├── 4774.0400000577856 │ └── zNormal.vtp ├── 4775.4600000578166 │ └── zNormal.vtp . . .
在进行后续分析之前,请确保案例模拟已完成且表面数据已成功提取。
表面数据提取为了从OpenFOAM生成的VTK文件中提取数据,我们将使用PyVista库。PyVista是可视化工具包(VTK)的Python接口,通过NumPy包装VTK库,提供了直接访问数组的方法和类。它为VTK的强大可视化后端提供了一个文档完善的Pythonic接口,便于快速原型设计、分析和空间参考数据集的可视化集成。
PyVista在科学计算可视化中具有重要价值,尤其适用于演示和研究论文的图形生成。同时它也作为其他依赖3D网格渲染的Python模块的支持库。
导入必要的模块,包括PyVista:
import matplotlib.colors import matplotlib.pyplot as plt import numpy as np import pandas as pd import fluidfoam as fl import scipy as sp import os import matplotlib.animation as animation import pyvista as pv import imageio import io %matplotlib inline plt.rcParams.update({font.size : 18, font.family : Times New Roman, "text.usetex": True})
接下来设置路径变量和常量:
### 常量d = 0.1 Ub = 0.015 ### 路径Path = E:/deephub/Sq_Cyl_Surfaces/surfaces/ save_path = E:/deephub/SquareCylinderData/ Files = os.listdir(Path)
现在可以尝试读取第一个快照表面:
Data = pv.read(Path + Files[0] + /zNormal.vtp) grid = Data.points x = grid[:,0] y = grid[:,1] z = grid[:,2] rows, columns = np.shape(grid) print(rows = , rows, columns = , columns) print(Data.array_names)
输出:
[TimeValue, p, U]
从输出可以看出,我们的二维切片包含了时间值、压力场和速度场。利用PyVista,可以为每个快照提取涡量场,并将结果数据组织成一个大型矩阵,以便进行后续的POD计算。具体实现如下:
Data = pv.read(Path + Files[0] + /zNormal.vtp) grid = Data.points x = grid[:,0] y = grid[:,1] z = grid[:,2] rows, columns = np.shape(grid) print(rows = , rows, columns = , columns) ### 对U场进行处理Snaps = len(Files) # 快照数量 data_Vort = np.zeros((rows,Snaps-1)) for i in np.arange(0,Snaps-1): data = pv.read(Path + Files[i] + /zNormal.vtp) gradData = data.compute_derivative(U, vorticity=True) grad_pyvis = gradData.point_data[vorticity] data_Vort[:,i:i+1] = np.reshape(grad_pyvis[:,2], (rows,1), order=F) np.save(save_path + VortZ.npy, data_Vort)
让我们检查一下生成的data_Vort数组的维度:
data_Vort.shape ### 输出### (96624, 1600)
此外,我们可以可视化涡量场的一个快照:
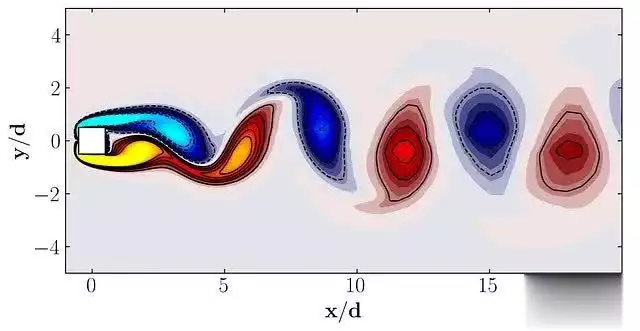
这个可视化结果展示了方形圆柱周围的涡量分布,为我们提供了流场结构的直观认识。
正交分解(POD)为了确定动态模态分解(DMD)的最佳近似秩,我们可以对涡量场数据进行正交分解(POD)分析。POD是一种强大的降维技术,能够捕捉流场中的主要能量结构。
以下是POD分析的Python实现:
### POD分析# 构建数据矩阵X = data_Vort # 计算并去除平均场X_mean = np.mean(X, axis = 1) Y = X - X_mean[:,np.newaxis] # 计算协方差矩阵C = np.dot(Y.T, Y)/(Y.shape[1]-1) # 对协方差矩阵进行奇异值分解U, S, V = np.linalg.svd(C) # 计算POD模态Phi_POD = np.dot(Y, U) # 计算时间系数a = np.dot(Phi_POD.T, Y)
接下来可以分析POD特征值以评估各模态的能量贡献:
Energy = np.zeros((len(S),1)) for i in np.arange(0,len(S)): Energy[i] = S[i]/np.sum(S) X_Axis = np.arange(Energy.shape[0]) heights = Energy[:,0] fig, axes = plt.subplots(1, 2, figsize = (12,4)) ax = axes[0] ax.plot(Energy, marker = o, markerfacecolor = none, markeredgecolor = k, ls=-, color = k) ax.set_xlim(0, 20) ax.set_xlabel(Modes)ax.set_ylabel(Energy Content)ax = axes[1] cumulative = np.cumsum(S)/np.sum(S) ax.plot(cumulative, marker = o, markerfacecolor = none, markeredgecolor = k, ls=-, color = k) ax.set_xlabel(Modes)ax.set_ylabel(Cumulative Energy)ax.set_xlim(0, 20) plt.show()
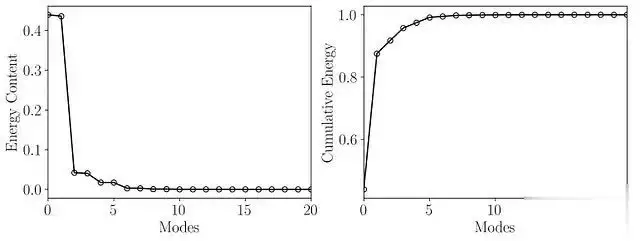
分析结果显示,前21个POD模态捕捉了约99.9%的总能量。这一发现为我们后面选择DMD的近似秩提供了重要依据,表明使用21阶近似进行DMD分析是合理的。
以下是前几个POD模态的可视化结果,用于参考:
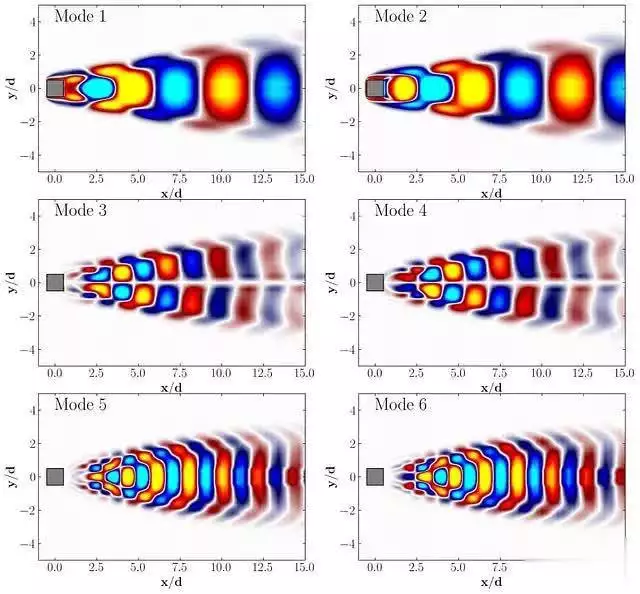
这些模态图展示了流场中的主要结构,为我们理解流动特性提供了直观的洞察。
动态模态分解(DMD)动态模态分解是一种强大的技术,能够提取流场中的动态特征。以下是DMD算法的Python实现:
def DMD(X1, X2, r, dt): # 对X1进行奇异值分解 U, s, Vh = np.linalg.svd(X1, full_matrices=False) # 截断SVD矩阵 Ur = U[:, :r] Sr = np.diag(s[:r]) Vr = Vh.conj().T[:, :r] # 构建Atilde矩阵并计算其特征值和特征向量 Atilde = Ur.conj().T @ X2 @ Vr @ np.linalg.inv(Sr) Lambda, W = np.linalg.eig(Atilde) # 计算DMD模态 Phi = X2 @ Vr @ np.linalg.inv(Sr) @ W # 计算连续时间特征值 omega = np.log(Lambda)/dt # 计算DMD模态振幅 alpha1 = np.linalg.lstsq(Phi, X1[:, 0], rcond=None)[0] b = np.linalg.lstsq(Phi, X2[:, 0], rcond=None)[0] # DMD重构 time_dynamics = None for i in range(X1.shape[1]): v = np.array(alpha1)[:,0]*np.exp( np.array(omega)*(i+1)*dt) if time_dynamics is None: time_dynamics = v else: time_dynamics = np.vstack((time_dynamics, v)) X_dmd = np.dot(np.array(Phi), time_dynamics.T) return Phi, omega, Lambda, alpha1, b, X_dmd
为了应用这个DMD函数,我们首先需要准备时间偏移的数据矩阵:
# 获取数据矩阵的两个时间步长偏移视图X1 = np.matrix(X[:, 0:-1]) X2 = np.matrix(X[:, 1:])
然后,我们定义近似秩和时间步长:
r = 21 # 根据POD分析结果选择dt = 0.01*142
接下来,我们执行DMD计算:
Phi, omega, Lambda, alpha1, b, X_dmd = DMD(X1, X2, r, dt)
在进行可视化之前,我们首先分析DMD特征值的分布。这有助于我们理解所识别的DMD模态的动态特性。我们将实部和虚部特征值绘制在单位圆上:
theta = np.linspace(0, 2 * np.pi, 150) radius = 1 a = radius * np.cos(theta) b = radius * np.sin(theta) fig, ax = plt.subplots() ax.scatter(np.real(Lambda), np.imag(Lambda), color = r, marker = o, s = 100) ax.plot(a, b, color = k, ls = --) ax.set_xlabel(r$\Lambda_r$) ax.set_ylabel(r$\Lambda_i$) ax.set_aspect(equal) plt.show()
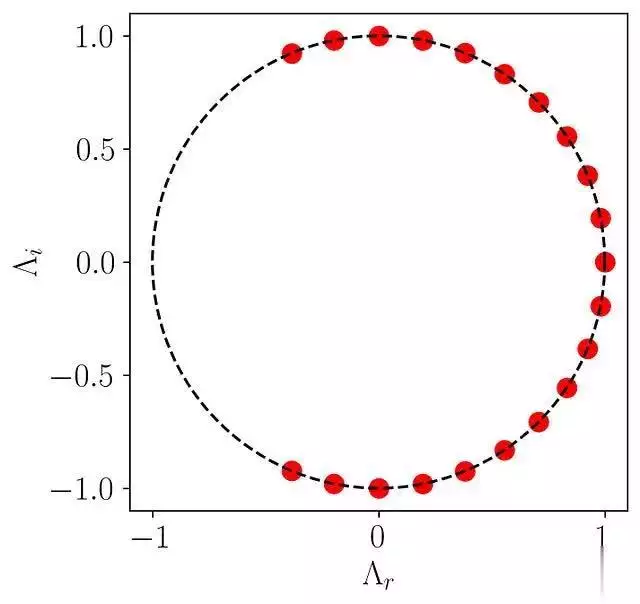
这个图显示所有特征值都位于单位圆上,表明DMD模态既不增长也不衰减,呈现稳定的特性。
为了可视化DMD模态,我们首先需要将DMD模态矩阵转换为数组:
A = np.squeeze(np.asarray(Phi))
然后可以使用Matplotlib绘制DMD模态:
Rect1 = plt.Rectangle((-0.5, -0.5), 1, 1, ec=k, color=white, zorder=2) Mode = 11 fig, ax = plt.subplots(figsize=(11, 4)) p = ax.tricontourf(x/0.1, y/0.1, np.real(A[:,Mode]), levels = 1001, vmin=-0.005, vmax=0.005, cmap = cmap) ax.add_patch(Rect1) ax.xaxis.set_tick_params(direction=in, which=both) ax.yaxis.set_tick_params(direction=in, which=both) ax.xaxis.set_ticks_position(both) ax.yaxis.set_ticks_position(both) ax.set_xlim(-1, 20) ax.set_ylim(-5, 5) ax.set_aspect(equal) ax.set_xlabel(r$\bf x/d$) ax.set_ylabel(r$\bf y/d$) ax.text(0, 4, r$f_i = + str(np.imag(Lambda[Mode])) + $, fontsize = 25, color = black) plt.show()
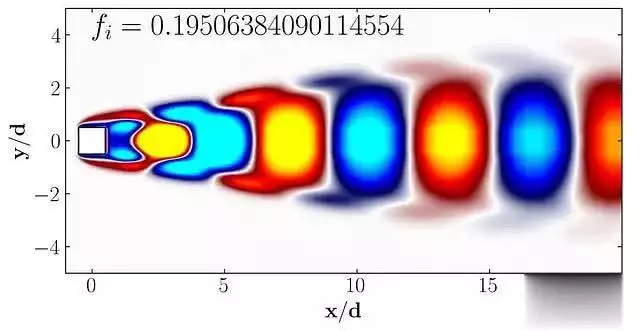
这个图展示了第11个DMD模态的空间结构。类似地,我们可以绘制前6个DMD模态:

这些DMD模态图揭示了流场中的关键动态结构,为我们深入理解方形圆柱周围的流动特性提供了重要依据。
通过结合POD和DMD分析,我们不仅捕捉了流场的主要能量结构,还揭示了这些结构随时间的演化特性。这种综合分析方法为复杂流动系统的研究提供了强大的工具,能够帮助我们更深入地理解流体动力学现象。
总结本文详细介绍了一种基于OpenFOAM和Python的流场动态分析方法。我们从OpenFOAM模拟数据的提取和处理开始,利用PyVista库高效地处理二维切片数据。通过正交分解(POD)成功捕捉了流场的主要能量结构,为动态模态分解(DMD)的应用奠定了基础。DMD分析进一步揭示了流场的动态特征,使我们能够深入理解方形圆柱周围的复杂流动现象。
这种结合OpenFOAM、POD和DMD的综合分析方法,不仅提高了对复杂流体系统的认识,还为流体动力学研究提供了强大的工具。Python的灵活性和效率在整个分析过程中发挥了关键作用,展示了其在科学计算和数据可视化方面的优势。



